In this tutorial I’m going to introduce you to memoization — a specific type of caching that is used as a software optimization technique. Caching is storing the results of an operation for later use. An example is the storing of browsing history in web browsers so that when an already visited site is visited again it loads faster, but when I talk about memoization in python, it is the caching of function output based on its input or parameters. Once you memoize a function, it will only compute its output once for each set of parameters you call it with, every call after the first, is quickly retrieved from a cache. In this tutorial, you’ll see how and when to use memoize with Python, so you can use it to optimize your own programs and make them run much faster in some cases.

Orginal Article Medium: Memoization in Python.

Why and When Should You Use Memoization?

Ideally, you will want to memoize functions that have a deterministic output for a specific input parameter(s) and more importantly expensive function (those that takes long and or much memory to compute). Example of a deterministic function will be the sqrt function to calculate the square root of input because it is sure to produce the same output no matter what. So sqrt(16) will always be 4, In this case, it makes sense to memoize this function given this input rather than re-computing the function with same parameter(s) over and over again. But an example of an expensive and deterministic function will be those implementing recursions, like Fibonacci, Factorial etc. These are where Memoization is needed to speed up part of these parts of the programs that slow it down and take away resources from your machine.

How to Memoize in Python?

Basic Memoization Algorithm

1. Set up a cache data structure for function results.
2. Every time the function is called, do one of the following: Return the cached result, if any; or Call the function to compute the missing result, and then update the cache before returning the result to the caller So there is a data structure to store all results. In our case, we will use a dictionary with the input parameter(s) as keys and the outputs as values. So every time a function is called it first checks whether the inputs exists in the cache if it does it returns the value else it computes the new output for the new input, updates the cache with the new input then it returns the output. Let see some examples now:

import timeit
def fibonacci(n):
	if n == 0:
		return 0
	elif n == 1:
		return 1
	return fibonacci(n - 1) + fibonacci(n - 2)

# average time taken is 15sec
# print(fibonacci(35))
print("Benchmark of fibonacci running time: ", timeit.timeit('fibonacci(35)', globals=globals(), number=1))

Running this program with the input of 35, fibonacci(35), it took an average of 15seconds to compute every time, though the output is sure to remain the same that is 9227465 for every run. What if we can store this results so that we don’t need to re-compute it again but rather and grab and use the result, that where Memoization comes in.

import timeit
cache = {}
def fibonacci(n):
	global cache
	if n in cache:
		return cache[n]
	else: 
		if n == 0: 
			return 0
		elif n == 1: 
			return 1
		else:
			cache[n] = fibonacci(n - 1) + fibonacci(n - 2)
			return cache[n] 
    
print("Benchmark of fibonacci running time: ", timeit.timeit('fibonacci(35)', globals=globals(), number=1))
print("Benchmark of fibonacci running time: ", timeit.timeit('fibonacci(35)', globals=globals(), number=1))
print("Benchmark of fibonacci running time: ", timeit.timeit('fibonacci(35)', globals=globals(), number=1))

Running the second program this time around, same fibonacci(35), it took an average of just 60microseconds to compute for the first time and just 2 microseconds for all subsequent calls of the function. You might have expected the first call to have taken 15seconds, this isn’t so because the Fibonacci function works by calling itself repeatedly and since from our function we are caching every value if it is new, we end up re-computing the same input values over again. See the diagram below for how Fibonacci recursion calls work.

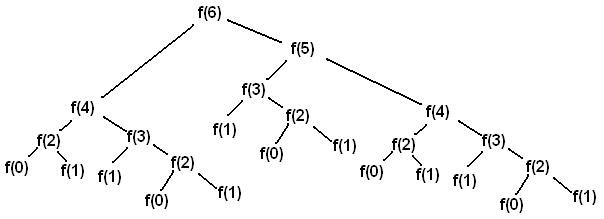Fibonacci binary recursion tree

Now let implement it using decorator function:

import timeit
import fibonacci from fibonacci

def memoize(func):
	cache = dict()
	def memoized_func(*args):
		if args in cache:
			return cache[args]
		result = func(*args)
		cache[args] = result
		return result
	
	return memoized_func

memoized_fibonacci = memoize(fibonacci) 

print("Benchmark of fibonacci running time: ", timeit.timeit('memoized_fibonacci(35)', globals=globals(), number=1))
print("Benchmark of fibonacci running time: ", timeit.timeit('memoized_fibonacci(35)', globals=globals(), number=1))
print("Benchmark of fibonacci running time: ", timeit.timeit('memoized_fibonacci(35)', globals=globals(), number=1)) 

Now running the program this time around, same fibonacci(35), it took an average of just 15seconds to compute for the first time as expected and just 2.5 microseconds on average for all subsequent calls of the function. This is because the decorator function caches only the final output and not all outputs along the computing line but all subsequent calls are all done in constant time.

Python Memoization with functools.lru_cache

Now that you’ve seen how to implement a memoization function yourself, I’ll show you how you can achieve the same result using Python’s functools.lru_cache decorator for added convenience. The lru_cache decorator is the Python’s easy to use memoization implementation from the standard library. Once you recognize when to use lru_cache, you can quickly speed up your application with just a few lines of code. Let’s revisit our Fibonacci sequence example. This time I’ll show you how to add memoization using the functools.lru_cache decorator:

import functools
import timeit

@functools.lru_cache(maxsize=128)
def fibonacci(n):
	if n == 0:
		return 0
	elif n == 1:
		return 1
	return fibonacci(n - 1) + fibonacci(n - 2) 

print("Benchmark of fibonacci running time: ", timeit.timeit('fibonacci(35)', globals=globals(), number=1))
print("Benchmark of fibonacci running time: ", timeit.timeit('fibonacci(35)', globals=globals(), number=1))
print("Benchmark of fibonacci running time: ", timeit.timeit('fibonacci(35)', globals=globals(), number=1))

Here again, the benchmark for fibonacci(35) was 10microseconds to compute for the first time and just 2microseconds for all subsequent calls of the function.The maxsize argument I’m passing to lru_cache to limit the number of items stored in the cache at the same time, as the cache data may get very large for bigger inputs. By decorating the fibonacci() function with the @lru_cache decorator I basically turned it into a dynamic programming solution, just as in the case of the second program where we implemented it using a global variable, where each subproblem is solved just once by storing the subproblem solutions and looking them up from the cache the next time. This is just a side-effect in this case — but I’m sure you can begin to see the beauty and the power of using a memoization decorator and how helpful a tool it can be to implement other dynamic programming algorithms as well.

Memoization in Python: Quick Summary

In this tutorial, you saw how Memoization allows you to optimize a function by caching its output based on the parameters you supply to it. Once you memoize a function, it will only compute its output once for each set of parameters you call it with. Every call after the first will be quickly retrieved from a cache You saw how to write your own memoization function from scratch, and why you probably want to use Python’s built-in lru_cache() battle-tested implementation in your production code.